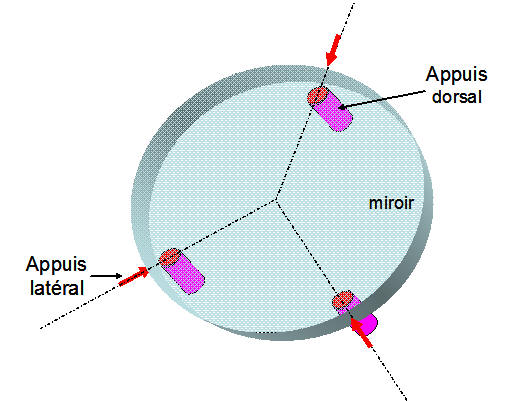
Barillets des miroirs primaires
1) La lois fondamentale pour les supports axiaux
2) Détermination du nombre de points d'appuis
3) Résumé des barillets avec leviers astatiques
5) Barillets avec supports triangulaires
6) Comparaison calculs Analytiques et PLOP
Le barillet du miroir doit maintenir le miroir de façon stable sans contraintes et éviter la déformation de l'optique sous son propre poids.
Le positionnement d'un solide dans l'espace nécessite 5 points fixes, 3 localisés sur le dos du miroir et 2 localisés sur la tranche du miroir. On met trois points sur la périphérie du miroir mais il n'y en a que deux qui portent simultanément sur la tranche suivant l'orientation du télescope. Le barillet le plus simple est donc représenté sur la figure 1 ci dessous:

figure1:
Cette structure composée de 3 points fixes dorsaux réglables et 3 butées latérales est nécessaire pour aligner l'axe optique du miroir dans le télescope mais cette structure est notablement insuffisante pour supporter l'immense majorité des miroirs d'amateurs d'aujourd'hui.
Contrairement à ce que l'on imagine intuitivement un miroir en verre fléchi de façon importante par rapport aux spécifications nécessaires sous son propre poids.
Les développements fondamentaux datent de la thèse d'André Couder [32]dont on peut trouver des éléments dans "lunettes et télescopes" [2] ou "la construction du télescope d'amateur" [3]. Dans ces deux derniers ouvrages on a les règles pratiques pour le design d'un barillet, les développements mathématiques sont explicités dans "reflecting telescope optique" [25].
Il est intéressant de comprendre l'origine des déformations et je vais donc expliciter un certain nombre de calculs qui font appel à la théorie de la déformation des plaques. Par ailleurs tout le monde aujourd'hui utilise un logiciel d'optimisation des barillets PLOP et je vous dirais ce qu'il faut en penser.
La difficulté des support provient du fait que la forme de la surface doit être maintenue quelque soit l'inclinaison du télescope avec une précision bien meilleur que lambda/4 qui représente environ 0.07 µm sur le verre c'est cette précision qui fait qu'un bloc de verre même très épais est extrêmement flexible. Les lois de la mécanique ne sont pas simples et une solution valable pour un miroir de 200mm de diamètre est complètement inopérante pour un miroir plus grand, il est intéressant de comprendre et de connaitre les lois d'échelles permettant de passer d'une taille de miroir à une autre.
1) La lois fondamentale pour les supports axiaux
On considère une plaque circulaire de rayon R qui fléchie sous une charge q uniforme (pression) repartie sur toute sa surface. Cette plaque est maintenue par son bord (elle repose sur un bord circulaire) cf figure 2 ci dessous
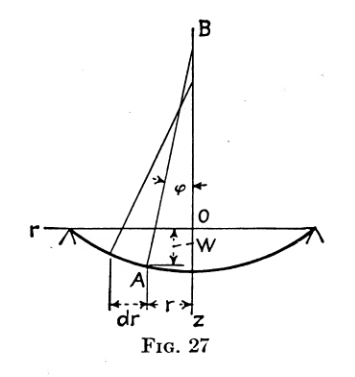
figure 2
dans ces condition la déflexion w qui dépends de r (distance du point sur le miroir par rapport au centre ) s'écrit:
W=q(R2 -r2)(KR2-r2)/64D (1)
avec D=Ee3/12(1-ν2) (2)
ou E est le module de Young du verre ,ν est le coefficient de poisson du verre (0.23) et e l'épaisseur du miroir
et K=(5+ν)/(1+ν) est un coefficient
l'équation (2) montre que D varie comme le cube de l'épaisseur e de la plaque
On voit avec l'équation (1) que si r=R (bord) la déformation est nulle et si r=0 (centre la déformation est maximum)
Wmax=3qK(1-ν2)/16E (R4/e3) (3)
Si maintenant la plaque n'est soumise qu'à son propre poids la plaque est soumise a une pression verticale q=gρe ou g est l'accélération de la pesanteur et ρ est la densité du miroir
on a alors
Wmax=3gρK(1-ν2)/16E (R4/e2) (4)
On trouve la fameuse loi de Couder (4) comme quoi la flexion d'un miroir sous l'effet de sont poids varie comme R4/e2
Le coefficient devant ne dépends que du matériau constitutif du miroir par l'intermédiaire de ( E, ν ) données mécanique et ρ sa densité
Les données pour quelques matériaux utilisés pour les miroirs sont rassemblées dans le tableau ci dessous
| matériau | module de young (1010 Pa) | module de poisson | densité 103(kg/m3) |
| verre (BK7) | 8.2 | 0.23 | 2.51 |
| Pyrex | 6.4 | 0.2 | 2.23 |
| quartz (silice fondue) | 7.45 | 0.17 | 2.2 |
| verre saint gobain | 6.0 | 0.22 | 2.45 |
| zerodur | 9.1 | 0.243 | 2.53 |
Si le support n'est plus sur le bord, mais à la distance rs= ξR du centre, l'équation (1) s'écrit avec r=uR
W=(1-ν2)gρ/E (R4/e2)(3/16V(u)-3/4U(u,ξ)) (5)
soit
W=Wm(3/16V(u)-3/4U(u,ξ)) (6)
Wm=(1-ν2)gρ/E (R4/e2) (7)
Wm est le facteur d'échelle qui dépends de la géométrie du miroir et des matériaux,
Les fonctions U et V valent:
U=2(1-u2)+((1-ν)/(1+ν))(1-ξ2)(1-u2)+2(u2+ξ2)ln(u) pour 0<ξ<u<1
U=2(1-ξ2)+((1-ν)/(1+ν))(1-ξ2)(1-u2)+2(u2+ξ2)ln(ξ) pour u<ξ<1
V=u4-(6+2ν)/(1+ν)u2+K
l'équation W/Wm est universelle est tracée figure 3 ci dessous pour diverse positions du cercle d'appuis.
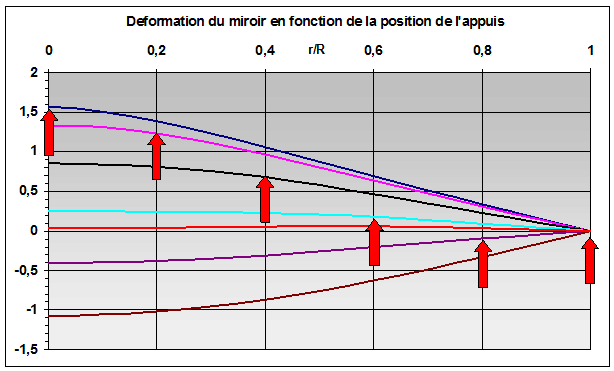
figure 3
Les flèches rouge représentent la position du cercle d'appuis pour chaque courbe, ξ (position de l'anneau support) varie de 0 à 1 par pas de 0.2. La courbe rouge est obtenue pour un rayon d'appuis de 0.66, elle présente une déformation minimale. Je reviendrais sur ce point. L'amplitude de la déformation est donnée par l'équation (7).
Ces équations ne résolvent pas complètement le problème du barillet car le miroir ne repose pas sur des anneaux mais sur des points fixes en nombre limités. Par ailleurs si Wm est important un seul cercle d'appuis n'est pas suffisant.
Pour un miroir supporté par deux couronnes de rayon ro=ξ0R et r1=ξ1R portant des charges respectives α =Po/Pmiroir et β=1-α on a:
W(u ,ξ0, ξ1)=3/4Wm[1/4V(u)-αU(u, ξ0)-(1-α)U(u, ξ1)] (8)
Pmiroir est le poids du miroir
La formule se généralise s'il y a plus de deux couronnes d'appuis avec des charges respectives α, β, γ, ... avec
α+β+γ+ ... =1
On optimise donc les charges et la position des couronnes pour minimiser W.
Dans le cas d'un miroir parabolique il est important de supprimer l'aberration de sphéricité introduite par la déflexion du miroir sous son poids. Cette aberration est représenté par le terme en ξ4 dans la formule (8). Il peut subsister une légère courbure (terme en ξ2) qui ne nuit pas à la qualité optique et qui ne fait qu'entraîner une légère modification de la focale.
Donc l'optimisation du barillet consiste avant tout à supprimer l'aberration de sphéricité induite par la flexion.
La stratégie suivit par A. Couder consiste a minimiser W au moyen de l'équation (8) c'est a dire trouver le nombre d'anneaux, leur position ξi et la fraction de poids (les coefficients α β ...) puis à remplacer les anneaux pleins par des points d'appuis en nombre limités. Le nombre de points par anneau est un multiple de 3 et est choisi suivant une règle que je préciserais.
Une règle supplémentaire souvent négligée est que l'anneau le plus extérieur est localisé à la périphérie du miroir.
La raison de ce choix est liée à l'astigmatisme que peuvent engendrer les butées latérales comme illustré figure 4 ci dessous. Si le point fixe dorsal est loin du point d'appuis latéral un couple Flatéral d important peut être généré induisant un astigmatisme du miroir. Si le point d'appuis est au bord d est petit et les forces de frottements sur le point d'appuis latéral n'induisent pas un couple important. Sur les miroirs dont disposent les amateurs une force latérale de quelques dizaines de grammes peut induire un astigmatisme gênant.
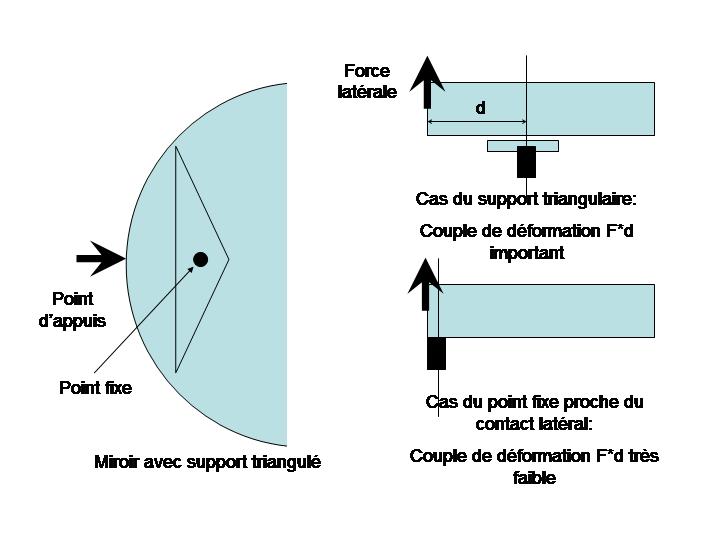
figure 4
Comme en général il faut plus de 3 points d'appuis et qu'un solide ne peut pas reposer sur plus de 3 points fixes des supports supplémentaires ont pour but d'appliquer des forces définies au dos du miroir. Il existe 2 systèmes pour multiplier le nombre de points d'appuis. Le système utilisé par Lord Ross (figure 5 ci dessous à gauche [32]) à savoir des structures triangulaires articulées au niveau de leur centre de gravité D, comportant 3 points d'appuis A, B, C. Dans ce cas les forces appliquées sur les points A B C sont identiques. Le système des triangles fonctionne bien lorsqu'il est constitué d'un seul étage de triangles, lorsque l'on empile plusieurs étages les problèmes de flexions et de contraintes résiduelles deviennent importants.
Le deuxième système est le système des leviers astatiques inventé par Lassel figure 5 de droite. Sur la figure le miroir repose sur 3 points fixes A et des forces réglables sont appliquées sous chaque point B.
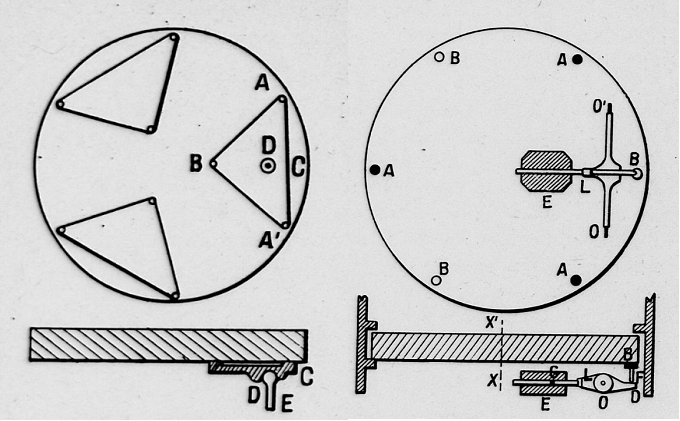
figure 5
Les forces sont données par l'intermédiaire de levier L dont les axes OO' sont supportés par le barillet. A l'une de leur extrémité ils sont muni d'un contrepoids E, l'autre extrémité presse sur le miroir par l'intermédiaire d'une bielle F et d'une touche. Si le centre de gravité G, l'axe OO' et l'articulation D sont situées dans un plan // au dos du miroir, chaque levier constitue un système astatique et l'effort est proportionnel à la composante du poids du miroir lorsque l'axe XX' n'est pas vertical.
La Force F appliquée par le levier est Mmass g cosZ Dm/D = F (9)
ou Z est l'angle du télescope par rapport au zénith
Mmass est la masse de la masselotte E
Dm/D le bras de levier
Dm= distance entre l'axe 00' et le centre de gravité de la masselotte
D = distance entre la biellette et l'axe OO'
Le réglage étant réalisé pour un angle du télescope (zénith) il est obtenu pour tout les angles, la stabilité mécanique et excellente.
On peut repartir les points B comme on veut et les multiplier autant que nécessaire. Un exemple de réalisation de levier astatique est donné ci figure 6:
figure 6
on peut trouver d'autres exemples de réalisation des leviers http://www.astrosurf.com/altaz/astatique.htm
2) Détermination du nombre de points d'appuis
La définition du barillet en suivant les développements de couder commence par définir comme on l'a vu le nombre d'anneau support en imposant un anneau sur le bord du miroir. Les flexions sont gouvernées par le rapport R4/e2
On calcul ce rapport avec R et e en cm
Si R4/e2<1000 (cm2) le barillet est des plus simple figure 7:
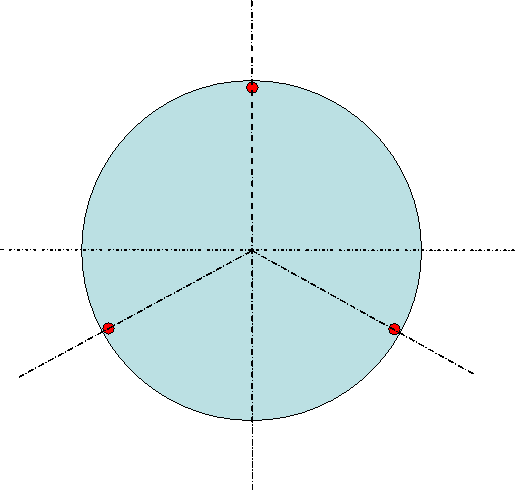
figure 7: Points d'appuis R4/e2<1000
Le problème de ce barillet provient de l'affaissement des bords du miroir entre les appuis comme on peut le voir sur la figure 8 de gauche ci dessous. L'écart sur l'onde du aux festons est de 60nm alors qu'au niveau radial c'est écart n'est que de 3nm (figure 8 de droite)
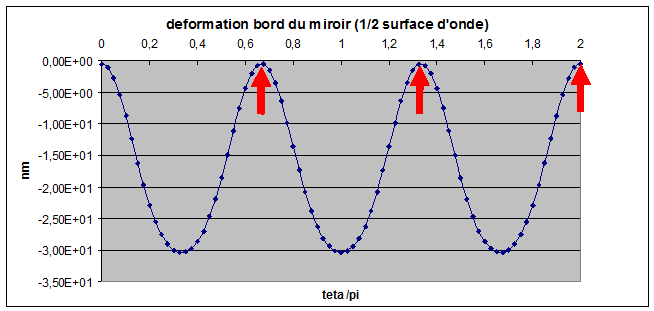
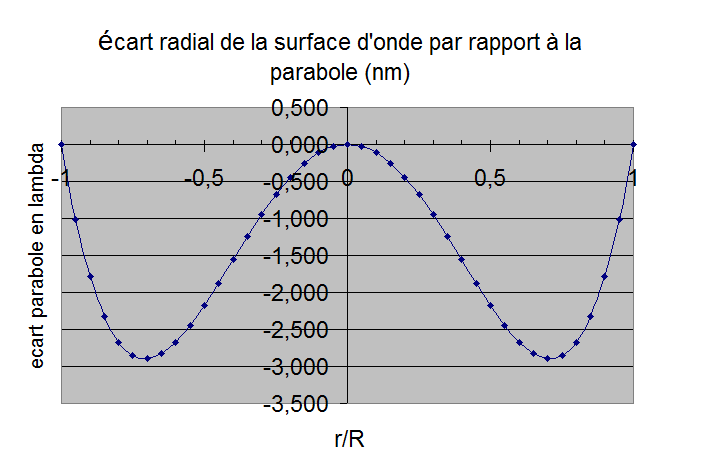
figure 8: Déformations d'un miroir avec R4/e2=1000 gauche feston sur le bord droite écart radial (en téta=0)
L'écart à la surface d'onde est de 60nm soit lambda/9 environ la déformation de la surface a une symétrie ternaire
On voit donc que pour aller au delà il faut rajouter avant tout des appuis sur le bord du miroir
Pour déterminer le nombre d'appuis ponctuels nécessaires pour remplacer l'anneau support, A. Couder donne la règle suivante:
m/n4 R4/e2<Wn (10)
ou m est la fraction du poids du miroir supporté par l'anneau (coef α β ...)
n nombre de point d'appuis sur l'anneau(ce que l'on cherche), n est toujours multiple de 3
Wn fonction empirique déterminée expérimentalement W3=12.3, W6=6.8, W9=5
Le calcul de la variation en téta de la déformation pour un miroir portant sur des appuis ponctuels périphériques est complexe, on trouvera ici la démonstration de la formule analytique utilisée.
Pour 6 appuis sur le bord (3 fixes en rouge et 3 leviers) on a figure 9
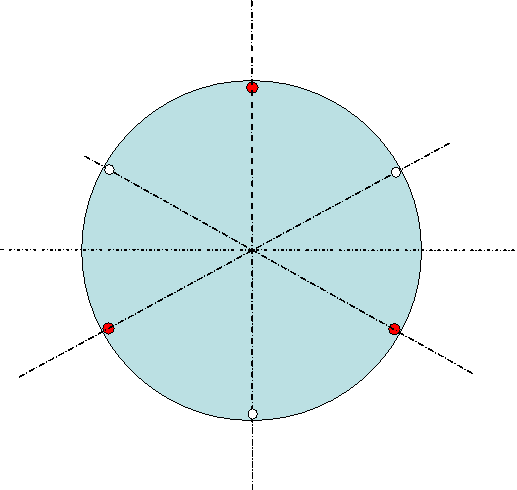
figure 9: Points d'appuis R4/e2<9000
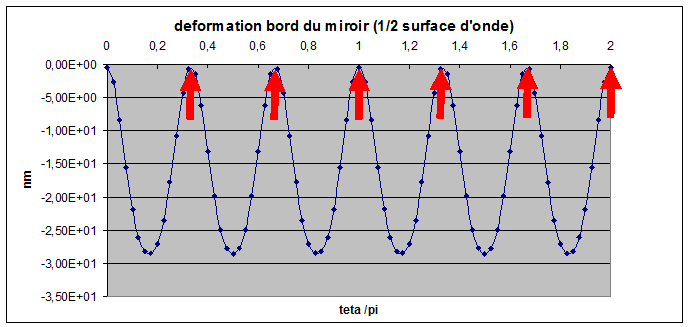
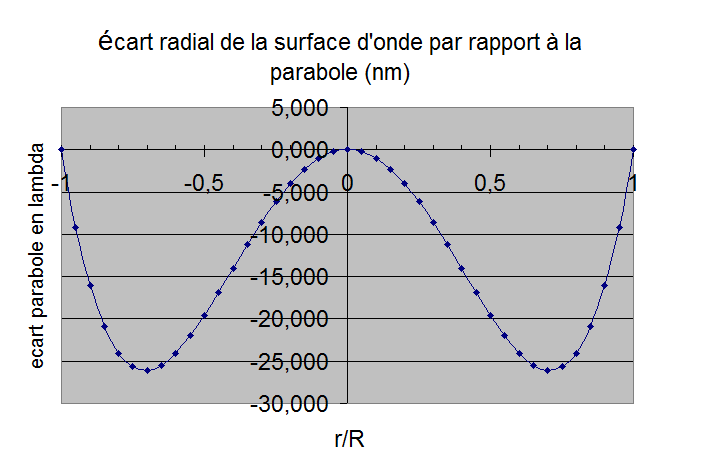
figure 10: Déformations d'un miroir avec R4/e2=9000 gauche feston sur le bord, a droite écart radial (en téta=0)
L'écart à la surface d'onde est de 60nm soit lambda/9 environ toujours sur le bord. Le miroir présente en plus une sous correction de lambda/20 et une variation de courbure de 0.25µm ce qui induit une variation du foyer. Ce type de barillet est utilisable jusqu'a R4/e2<9000
Si le miroir est un miroir plan utilisé en incidence oblique il faut supprimer le terme de courbure (en ξ2) avant le terme d'aberration sphérique. Pour ce faire il faut rajouter une force centrale figure 11 qui fait 0.404Pmiroir le réglage dans ce cas est correcte jusqu'a R4/e2<2800
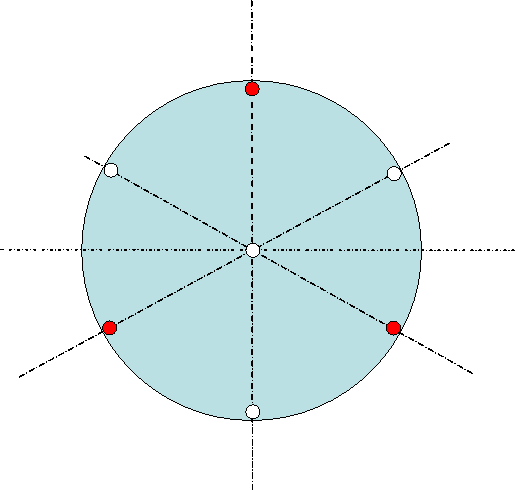
figure 11: Points d'appuis R4/e2<12000
pour un miroir parabolique l'appuis central exerce une force de 0.179Pmiroir
Dans ce cas la forme du miroir est correcte jusqu'a R4/e2=12000
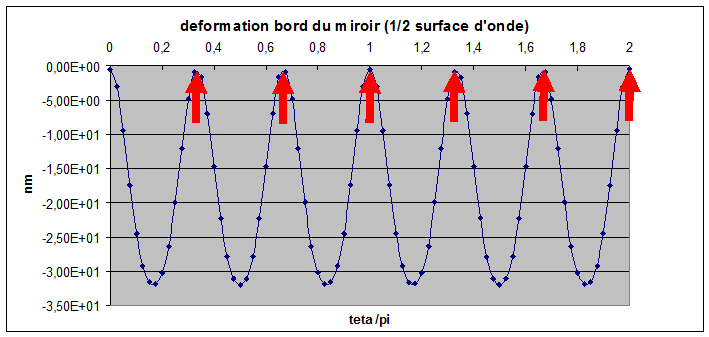
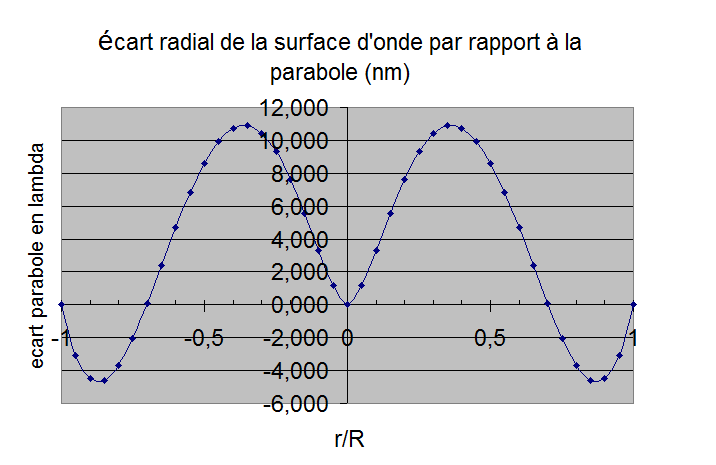
figure 12: Déformations d'un miroir avec R4/e2=12000 et une force centrale de 0.179Pmiroir gauche feston sur le bord, à droite écart radial (en téta=0)
Après optimisation dans PLOP la charge au centre est portée à 0.34P ce qui fourni une erreur RMS de 6.4nm au lieu de 8nm (sur l'onde)
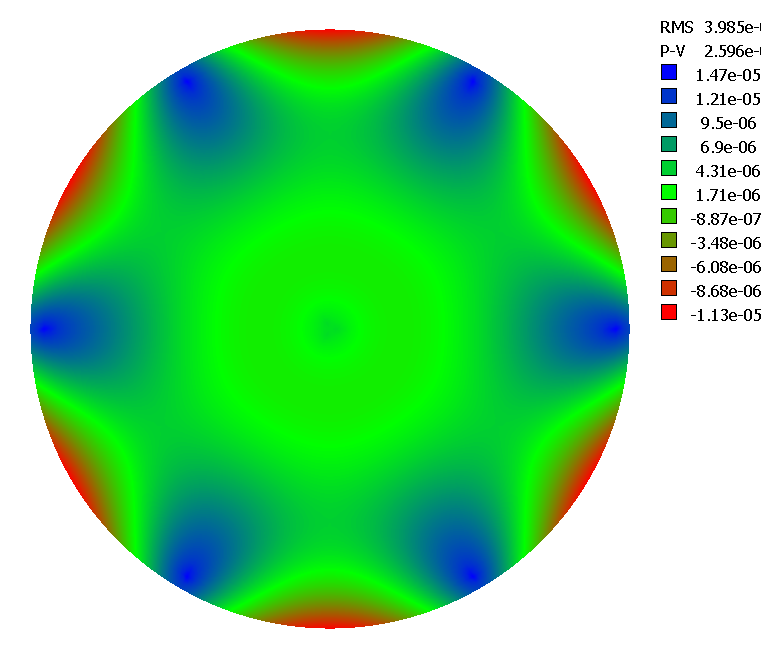
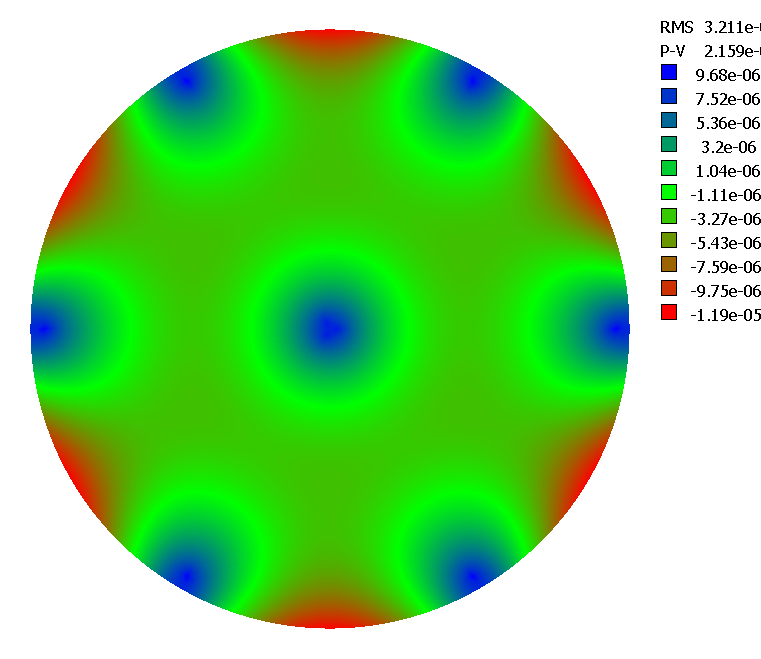
Pour aller jusqu'a R4/e2=45000 il faut arranger les leviers sur deux cercles (figure 13), le cercle interne étant à 1/3 du rayon du miroir et le poids porté par ce cercle étant de 0.3Pmiroir . C'est ce type de barillet que j'ai réalisé pour mon télescope de 500mm.
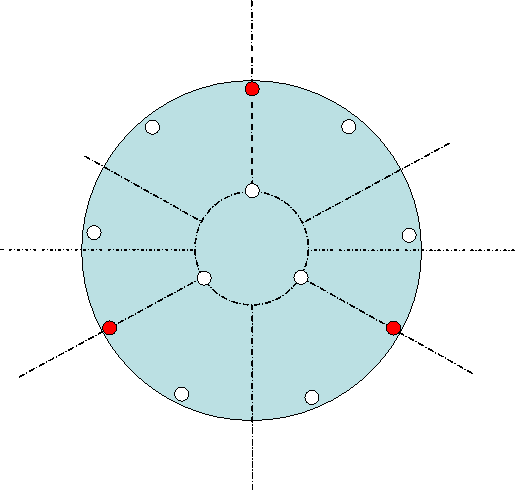
figure 13: Points d'appuis R4/e2<45000
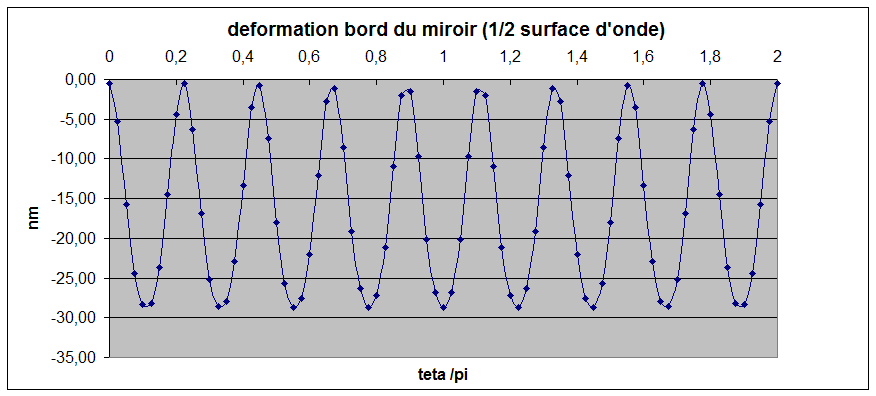
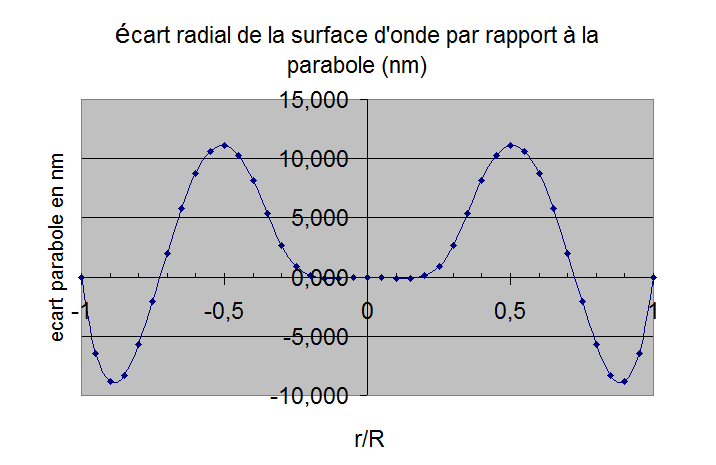
figure 14: Déformations d'un miroir avec R4/e2=45000 gauche feston sur le bord, à droite écart radial (en téta=0)
le calcul PLOP avec ces paramètres
rayon des anneaux 0.33 et 0.95
Forces 0.3P et 0.7P fourni une erreur RMS de 10nm sur l'onde et une erreur
PV de 68nm
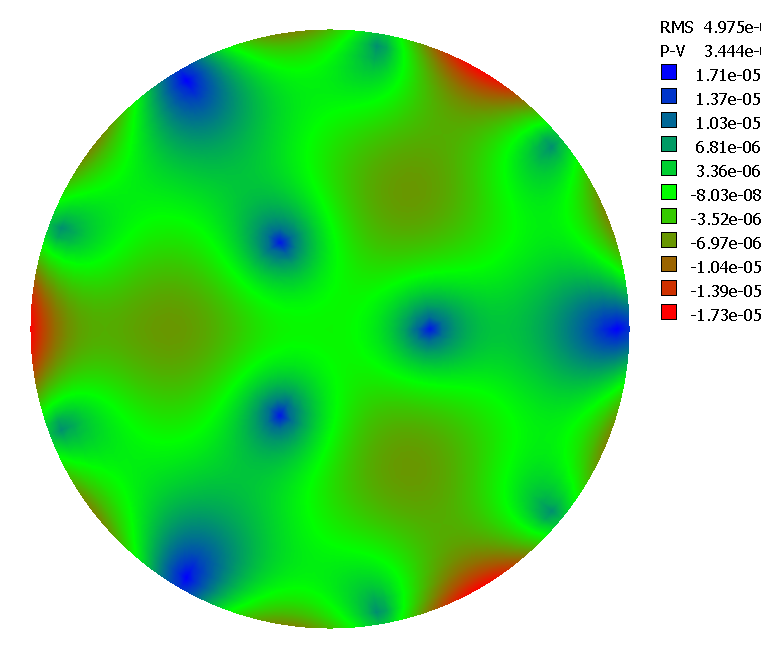
avant et après optimisation
Après optimisation il est intéressant de diminuer la force sur les appuis fixes pour égaliser les fluctuations sur la périphérie l'erreur RMS est alors de 7.4nm et l'erreur PV de 50nm (sur l'onde)
Rayon des anneaux 0.30 0.95
Force 0.279P et 0.721P dont 0.2295P sur les 3 points fixes
Pour aller jusqu'a R4/e2=90000 (miroir de 600mm et de 3cm d'épaisseur) il faut arranger les leviers sur deux cercles (figure 15), le cercle interne étant à 1/2 du rayon du miroir et le poids porté par ce cercle étant de 0.636Pmiroir .
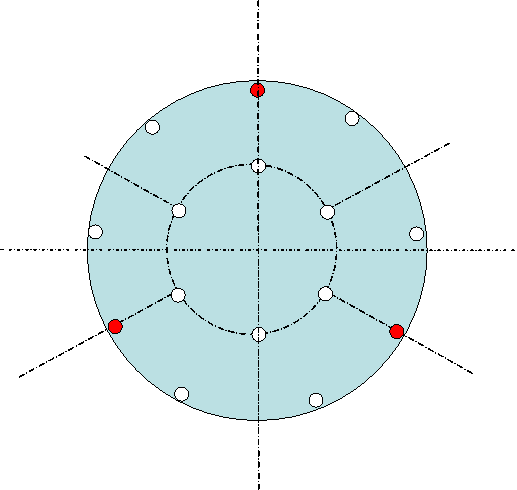
figure 15: Points d'appuis R4/e2<90000
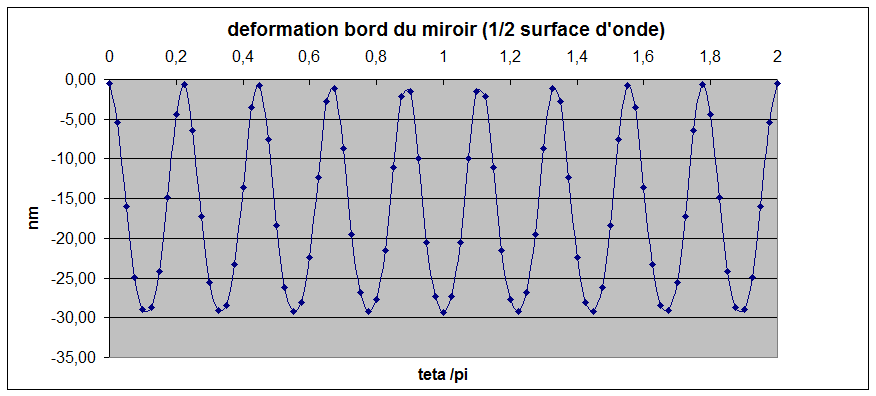
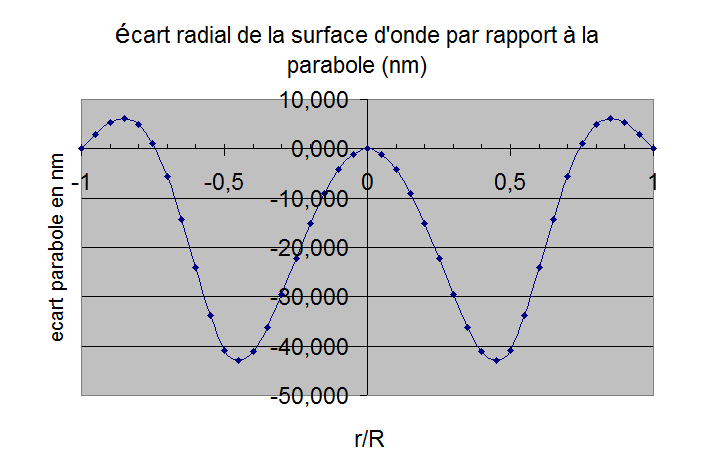
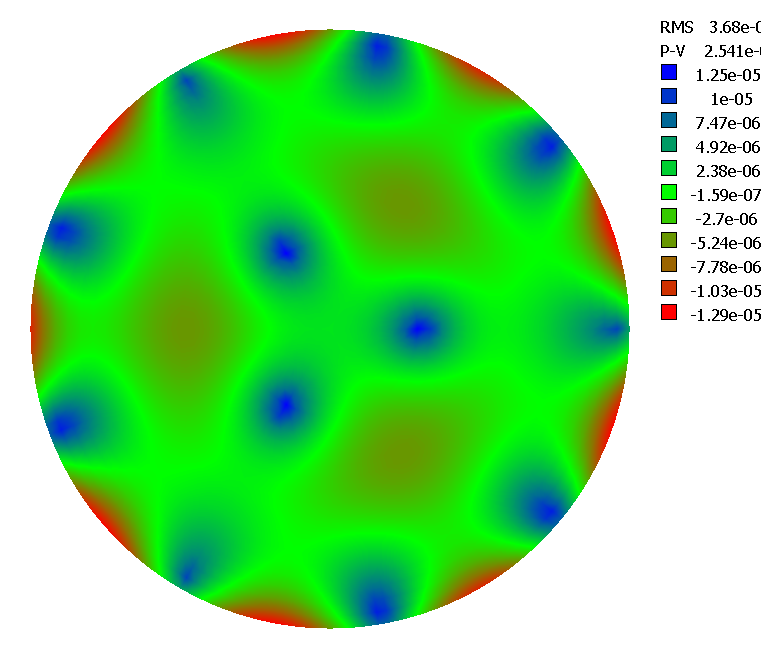
figure 16: Déformations d'un miroir avec R4/e2=90000 gauche feston sur le bord, à droite écart radial (en téta=0)
le calcul PLOP avec rayons support 0.5 0.95
poids par anneau 0.636, 0.364 pour un miroir 600mm e=42mm écart RMS 12.6nm
écart PV 80nm sur l'onde (ces valeurs sont sur évaluées car le module 3D
de plop ne fonctionne pas dans ce cas)
L'optimisation avec PLOP :
Rayons support 0.43 0.95
poids par anneau 0.532, 0.468 écart RMS 9.6nm écart PV 60nm sur l'onde
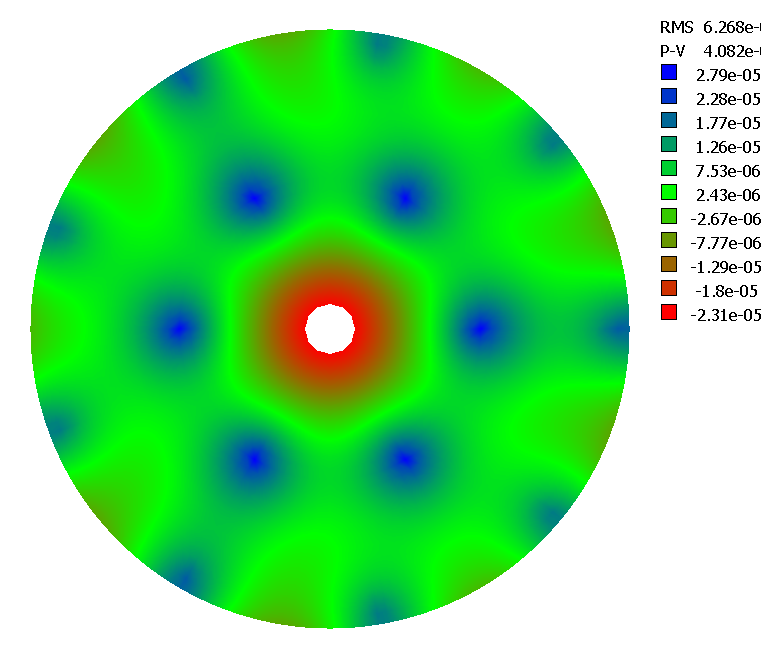
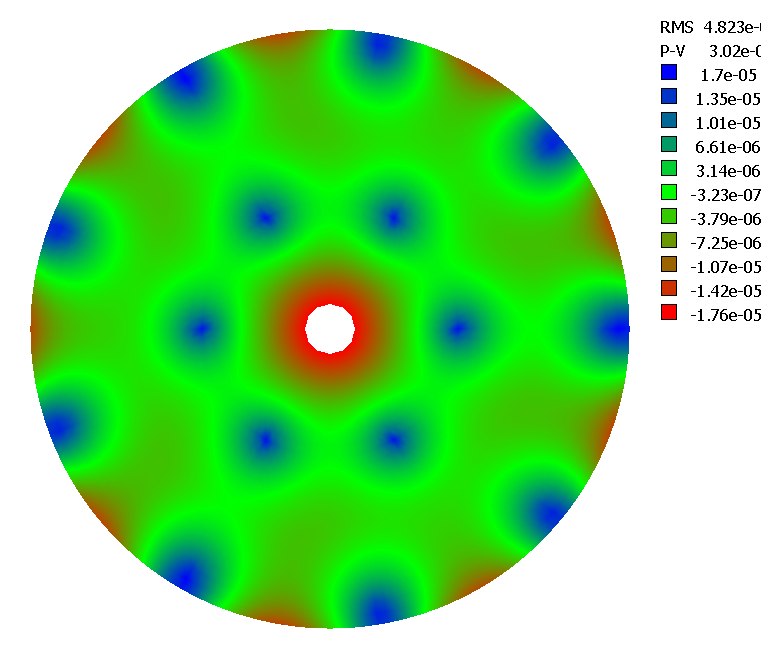
Avant et après optimisation PLOP
3) Résumé des barillets avec leviers astatiques
(précision surface d'onde >lambda/9):
Pour définir un barillet, le paramètre à calculer est le rapport R4/e2 de son miroir puis de se rapporter au tableau ci dessous
| R4/e2 < | nombre d'appuis cercle ξ=1 | poids sur le cercle externe | rayon du deuxième cercle | poids sur le deuxième cercle | nombre d'appuis deuxième cercle |
| 1000 | 3 | P | / | / | 0 |
| 9000 | 6 (3+3) | P | / | / | 0 |
| 12000 | 6 (3+3) | 0.821P | 0 | 0.179P | 1 |
| 45000 | 9 (3+6) | 0.7P | 0.3 | 0.3P | 3 |
| 90000 | 9 (3+6) | 0.344P | 0.5 | 0.636P | 6 |
Le tableau ci dessus couvre la très grande majorité des miroirs d'amateur. Pour aller au delà il faut rajouter un troisième cercle.
Le programme d'optimisation ici permet de calculer un barillet dans ce cas, ou permet de calculer la déformation pour une valeur donnée des paramètres du miroir.
Après optimisation avec PLOP on a les paramètres suivants:
|
R4/e2 < |
nombre d'appuis cercle ξ=1 | poids sur le cercle externe | rayon du deuxième cercle | poids sur le deuxième cercle | nombre d'appuis deuxième cercle |
| 1000 | 3 | P | / | / | 0 |
| 9000 | 6 (3+3) | P | / | / | 0 |
| 12000 | 6 (3+3) | 0.66P | 0 | 0.34P | 1 |
| 45000 | 9 (3+6) | 0.721P | 0.3 | 0.279 | 3 |
| 90000 | 9 (3+6) | 0.468P | 0.43 | 0.532P | 6 |
Les différences en terme de résultat avant et après optimisation sont faibles ce qui montre que l'on a une certaine latitude de réglage.
Pour avoir le poids à appliquer par touche il faut diviser le poids du cercle par le nombre d'appuis du cercle (y compris les appuis fixes)
Pour avoir le poids de la masselotte sur les leviers il faut diviser le poids de l'appuis par le bras de levier.
Les appuis latéraux doivent maintenir le miroir en place lorsque le télescope pointe avec un angle zénithal non nul. Il doivent éviter le glissement du miroir sur les appuis dorsaux et la formation de forces parallèles au dos du miroir présentant plus ou moins d'hystérésis.
Pour se faire il faut que les points dorsaux génèrent très peu de friction, que les appuis latéraux soient très rigides et ne génèrent pas de forces parallèle à la tranche du miroir.
Le calcul théorique de l'astigmatisme induit par les supports latéraux est complexe car il dépends de données difficiles à appréhender comme les forces de frictions sur les appuis. Un cas calculable est celui induit par le poids du miroir et la forme du miroir lorsqu'il est en position verticale. Ce cas constitue un minimum et toute imperfection dans la réalisation ne fera qu'augmenter la déformation.
Les appuis les plus performant sont réalisés avec des roulettes ou roulements à billes qui portent sur la tranche. La roulette est // à l'axe optique pour que le miroir puisse descendre librement sur ses appuis dorsaux.
Pour un Dobson ou télescope azimutal l'écartement optimum entre les 2 roulettes est de 90° figure 17, pour un équatorial cet angle est de 120°
La roulette ne doit pas être trop petite car le couple de friction sur l'axe du roulement sera atteint pour une force latérale le long du miroir plus faible si la roulette a un diamètre important. Le point d'appuis de la roulette doit être dans le plan contenant le Centre De Gravité du miroir qui se trouve plus bas que la moitié de l'épaisseur du miroir à cause de la face concave. En cas de doute il vaut mieux être un peu au dessus qu'au dessous du CDG.
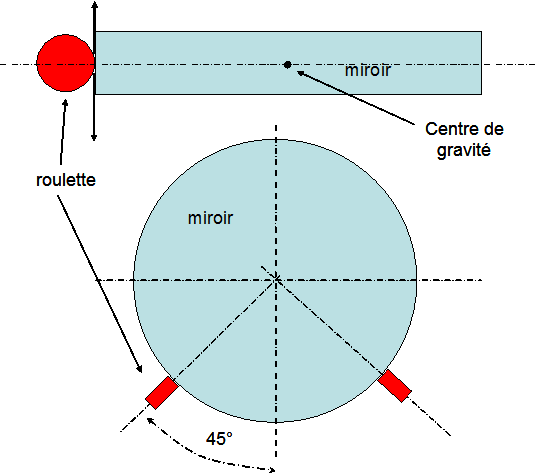
figure 17: appuis latéral
Pour les gros miroirs très lourd on peut remplacer la roulette simple par deux roulettes portées par un étrier articulé .

5) Barillets avec supports triangulaires
Ce type de barillet peut paraître plus simple à réaliser que le système des leviers par contre cette simplicité est trompeuse.
Couder pense que la solution la plus simple figure 5 à gauche est valable jusqu'a R4/e2=13000
Dans ce cas, l'optimum est obtenu pour un rayon interne de 0.34R (0.32R suivant plop) la déformation est calculée ci dessous
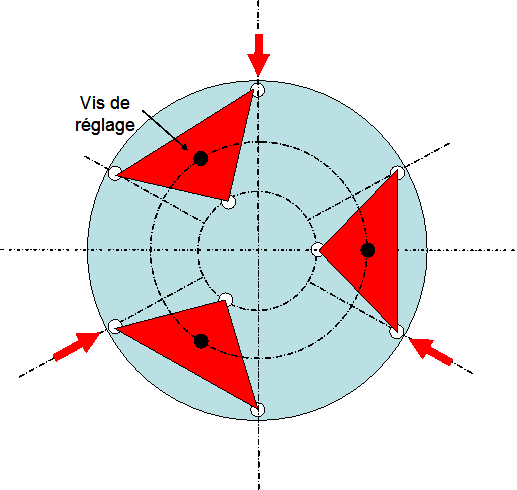
figure 18: barillet à base de triangles pour R4/e2<13000
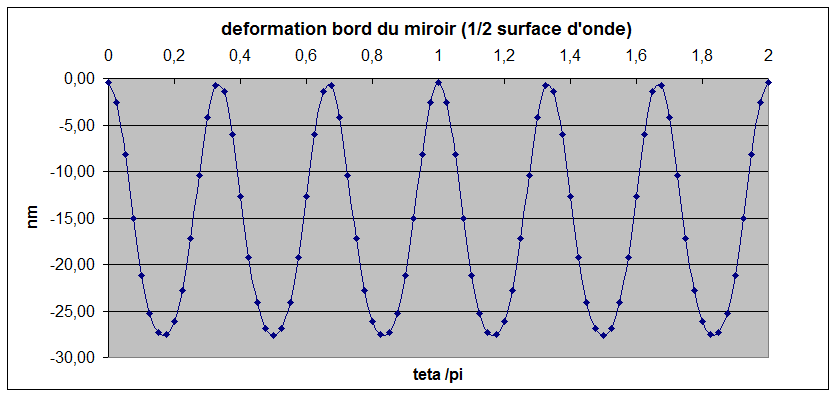
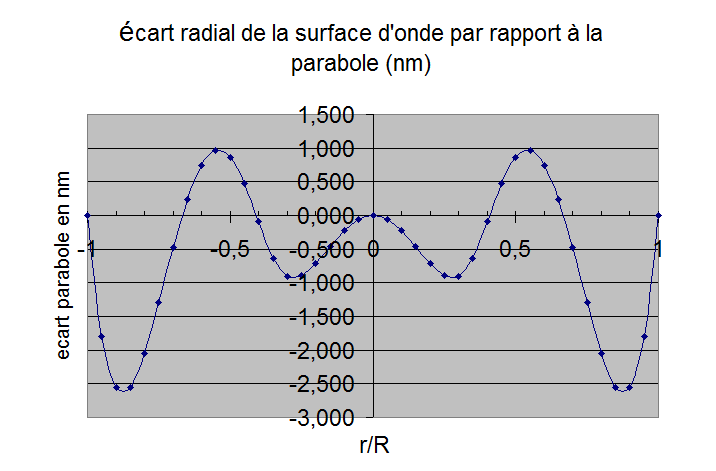
figure 19: Déformations d'un miroir avec R4/e2=13000 pour un support avec 3 triangles, à gauche feston sur le bord, à droite écart radial (en téta=0)
Lorsque l'on empile les triangles sur plusieurs étages, les problèmes de réalisation, de flexibilité de l'empilement et d'astigmatisme généré par les appuis latéraux augmentent.
Le programme PLOP permet d'optimiser un barillet réalisé à base de supports triangulaires. Les optimisations généralement conduisent à grouper les points d'appuis autour du rayon 0.66R et ne conduisent pas à des points proches du bord ce qui n'est pas du tout optimum pour gérer l'astigmatisme induit par le barillet (appuis latéraux). On optimise uniquement l'aberration de sphéricité au détriment des autres aspects qui peuvent devenir prépondérant et complètement échapper au calcul.
Il ne faut donc pas être obsédé par les simulations de PLOP, le programme n'est pas parfait et ne tient pas compte des forces de frictions donc
un support plus facile à réaliser et qui donne des écarts faibles par rapport à une solution plus compliquée sera meilleur.
Les points critiques outres les appuis latéraux sont:
_La rigidité mécanique de l'empilement en z car tout le poids (variable en fonction de l'inclinaison) est porté par les 3 axes de réglages.
_Un triangle de sustentation du miroir plus petit que dans le cas des leviers.
_Le blocage en rotation des triangles (pour assurer le positionnement précis des appuis) tout en permettant un effet rotule très souple au niveau des axes de réglage.
Il ne faut jamais coincer (contraindre) un miroir dans son support, il ne doit pas être ajusté mais il faut laisser un jeu dans toutes les directions.
Il faut utiliser des points de contact avec peu de friction réalisés en plastic dure (delrin, nylon) et pas en téflon, on doit pouvoir tourner le miroir dans son barillet sans problèmes.
Les points d'appuis en liége sont à proscrire,
Tout les éléments du barillet qui pivotent doivent être réalisés avec peu de friction (utiliser des roulements et des composants de qualité) et le miroir doit être centré de façon précise dans le barillet .
6) Comparaison calculs Analytiques et PLOP
Des simulations avec PLOP pour un miroir en verre ordinaire de 300mm de diamètre de 42mm et 20mm d'épaisseur. Les résultats de PLOP sont systématiquement légèrement plus pessimistes que le calcul analytique. L'accord est bon (cf tableau ci dessous) si on met les appuis à 95% du rayon du miroir au lieu de 100%. Ce n'est pas très étonnant car la description d'un appuis ponctuel n'est pas très facile numériquement et le maillage de plop n'est pas adaptatif autour des points d'appuis. Un point est clair il faut absolument utiliser le module Z88 (3D) de plop sinon l'écart est relativement important. N'ayant pas d'infos particulières sur plop il est difficile de statuer sur l'origine des écarts. Comme on se donne un budget d'erreur assez loin de la limite de 1/4 d'onde les écarts sont faibles et la simulation des barillets avec leviers non couverte par PLOP avec le fichier Excel fourni sur le site peut être considérée comme correcte.
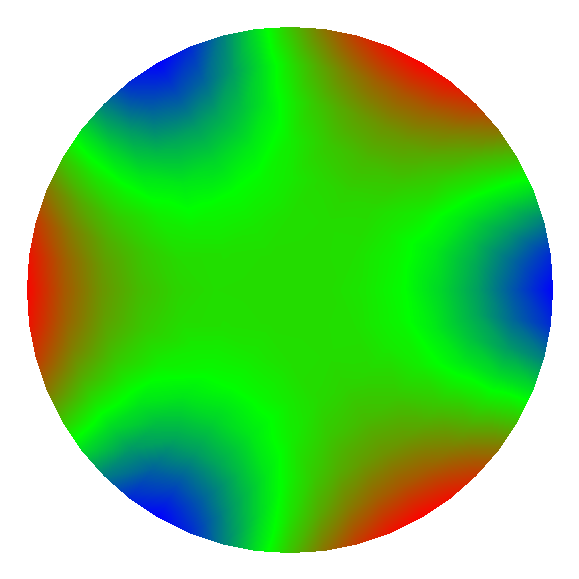
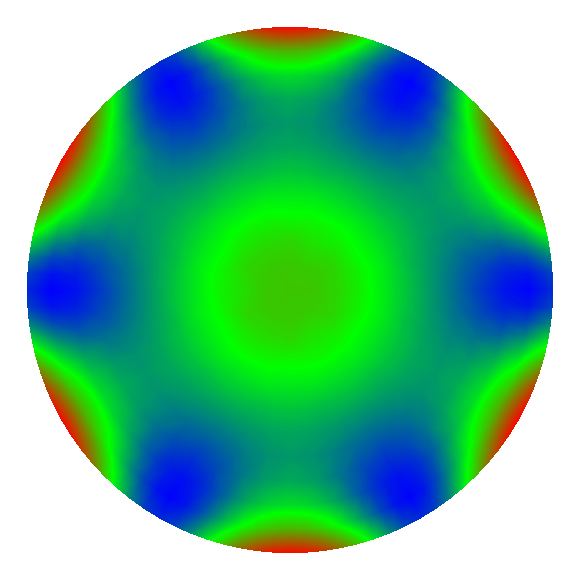
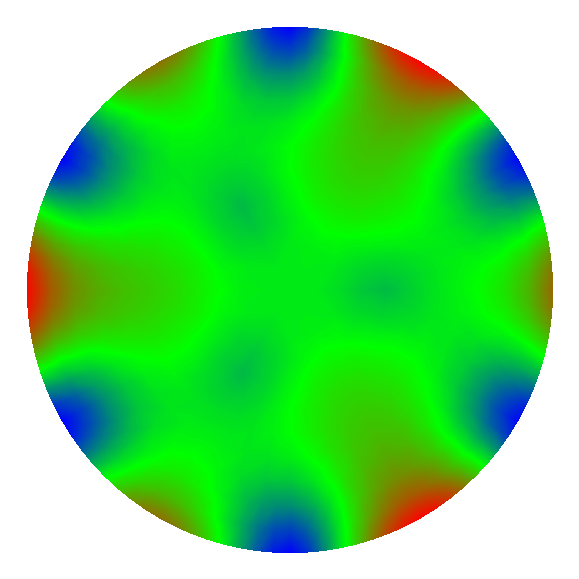
Figure 20: Résultats calcul de PLOP pour des supports 3, 6, 9 points avec les points d'appuis sur la périphérie du miroir (0.95 Rmiroir).
| R4/e2 | PLOP PV nm | Analytique PV nm | Ep mirroir mm | barillet |
| 2870 | 111 | 106 | 42 | 3points |
| 2870 | 15 | 11 | 42 | 6 points |
| 12656 | 34 | 33 | 30 | 9 points (triangles) |
Comparaisons erreur PV sur la surface même miroir même barillet PLOP et Analytique
7) Solution générale pour des supports sur 2 cercles
La solution analytique pour un cercle ayant un nombre quelconque de supports existe [33] on peut donc calculer la déformation d'un miroir supporté sur deux cercles de points (voir plus) en superposant les solutions pour chaque cercle.
Les équations sont écrites dans le document suivant.
Une feuille Excel permet de calculer la déformation pour une configuration donner et le solveur de la feuille permet d'optimiser le rayon des cercles et le poids à mettre sur chaque point d'appuis. On retombe sur le fait que le calcul comme plop n'évalue pas les problèmes d'astigmatisme induits par les supports latéraux s'ils sont mal réalisés (utiliser si possible des étriers).
La feuille de calcul est ici.
Il faut rentrer les données suivantes matériaux, miroir, barillet correspondant au cas considéré par exemple:
données matériaux Module de young 6.40E+10 Pa coef de poisson 0.2 densité 2.23 g/cm3 données miroir épaisseur du miroir 3 cm diamètre du miroir 30 cm données barillet nombre de points sur l'anneau extérieur 6 diamètre de l'anneau extérieur 19.62768186 cm nombre de points sur l'anneau intérieur (*) 3 diamètre de l'anneau intérieur 5.105409522 cm pourcentage du poids anneau extérieur 0.885199698 (*) cette valeur ne doit pas être nulle >=2
Exemple 1:
calcul pour un système de 3 triangles dans ce cas le poids porté par le cercle extérieur est 2/3 du poids du miroir, le solveur ne doit optimiser que sur les rayons des 2 cercles de points.
Il faut dans les cellules variable du solveur rentrer uniquement la cellule $C$49 la cellule $C$47 reste fixe à Rmax
Dans ce cas le solveur trouve un optimum pour Rint=0.33Rmiroir en accord avec les résultats du paragraphe 5.
Si on optimise sur les 2 rayons (les cellules variable du solveur sont la cellule $C$49 et la cellule $C$47 )
on trouve: Rext=0.76Rmiroir Rint=0.35Rmiroir écart PV 6.4nm
la solution PLOP: Rext=0.735Rmiroir Rint=0.34Rmiroir écart PV 7nm
La feuille de calcul est en accord avec PLOP
Exemple 2:
même système 6 points extérieur 3 points intérieur avec des leviers astatiques:
(les cellules variable du solveur sont les cellules $C$49; $C$47;$C$50 )
Rext=0.654Rmiroir Poids P1=0.85 Rint=0.17Rmiroir Poids P2=0.15 =(1-P1) écart PV 3.3nm 2 fois meilleur que la solution triangle
La feuille permet de calculer des barillets non implantable facilement avec PLOP.
© Jean DIJON : Tous les documents présents sur ce site sont
protégés par les lois sur les droits d'auteur.
La reproduction et la diffusion de ces documents sont interdites sans le
consentement de l'auteur.